Valeurs extrêmes en SHS

Journée MAD - 26/05/2025

Nicolas Pillaud

LabPsy - UR4139, Université de Bordeaux

Solenne Roux

LabPsy - UR4139, Université de Bordeaux & Réseau so-maté

Outliers - définition

Valeurs extrêmes ou Valeurs aberrantes ?

Outliers - pourquoi cette question ?

Tout démarre de notre pratique

Outliers - pas simple de répondre à cette question

Aguinis et al. 2013 proposent 14 définitions différentes

Extraits :

Valeur extrême par construction : Valeurs inhabituellement grandes ou petites par rapport aux autres valeurs du même construit. En général, en queue(s) de distribution.
Valeur extrême d’intérêt : Des points de données précis qui se trouvent à distance des autres points de données et qui peuvent contenir des informations valables ou des connaissances inattendues.
Valeur extrême liées à des analyses (modèles, cluster, etc.) : par exemple, valeurs extrêmes résultant de la conduite d’une analyse en cluster.

Outliers - pas simple de répondre à cette question

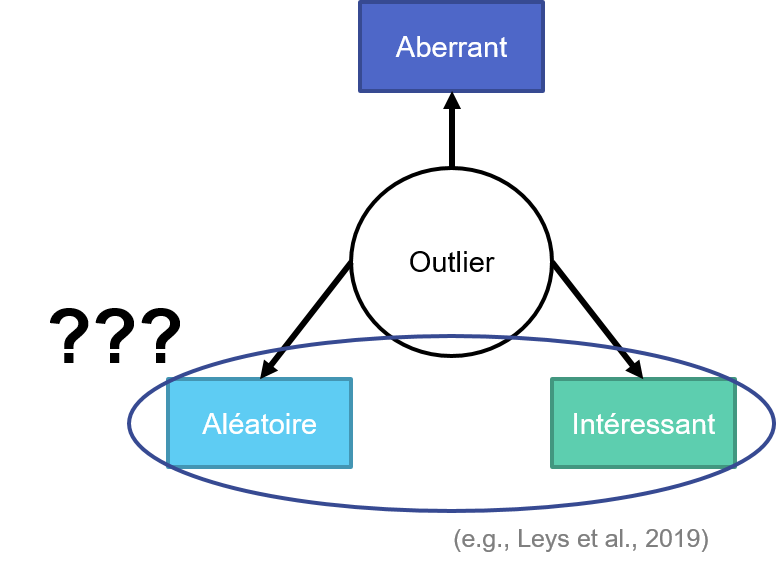
Outliers - la définition que nous choisissons

“An outlying observation, or”outlier,” is one that appears to deviate markedly from other members of the sample in which it occurs.” (Grubbs, 1969, p. 1)

“The intuitive definition of an outlier would be an observation that deviates so much from other observations as to arouse suspicion that it was generated by a different mechanism” (Hawkins, 1980, p. 1)

Outliers - comment sont-ils produits ?

Erreur liée aux outils de mesure
Erreur dans la manipulation des données
Erreur dans l’échantillonnage
Erreur humaine
Pas une erreur

Outliers - quels impacts ?

Catastrophique (Cowell & Victoria-Feser, 1996a)

Outliers - quels impacts ?

Négligeable (Cowell & Victoria-Feser, 1996b)

Outliers - quels impacts ?

Ca dépend (André, 2022; Hlasny & Verme, 2018; Karch, 2023)

Première partie : Outliers dans le cas de designs simples

Comparaison des méthodes de détection des valeurs extrêmes sur des designs simples (univariés ou bivariés).

Travaux d’un groupe de travail interne au LabPsy :

N. Pillaud, S. Roux, B. Subra, T. Alexopoulos & F. Ric

Première partie : Outliers dans le cas de designs simples

Comparaison de 7 méthodes de détection :

1.5 SD
3 SD
2.5 MAD
3 MAD
1.5 IQR
3 RSS
4 RSS

Première partie : Outliers dans le cas de designs simples

Comparaison des méthodes sur 3 designs :

Inter-groupes
Intra-groupes
Corrélations

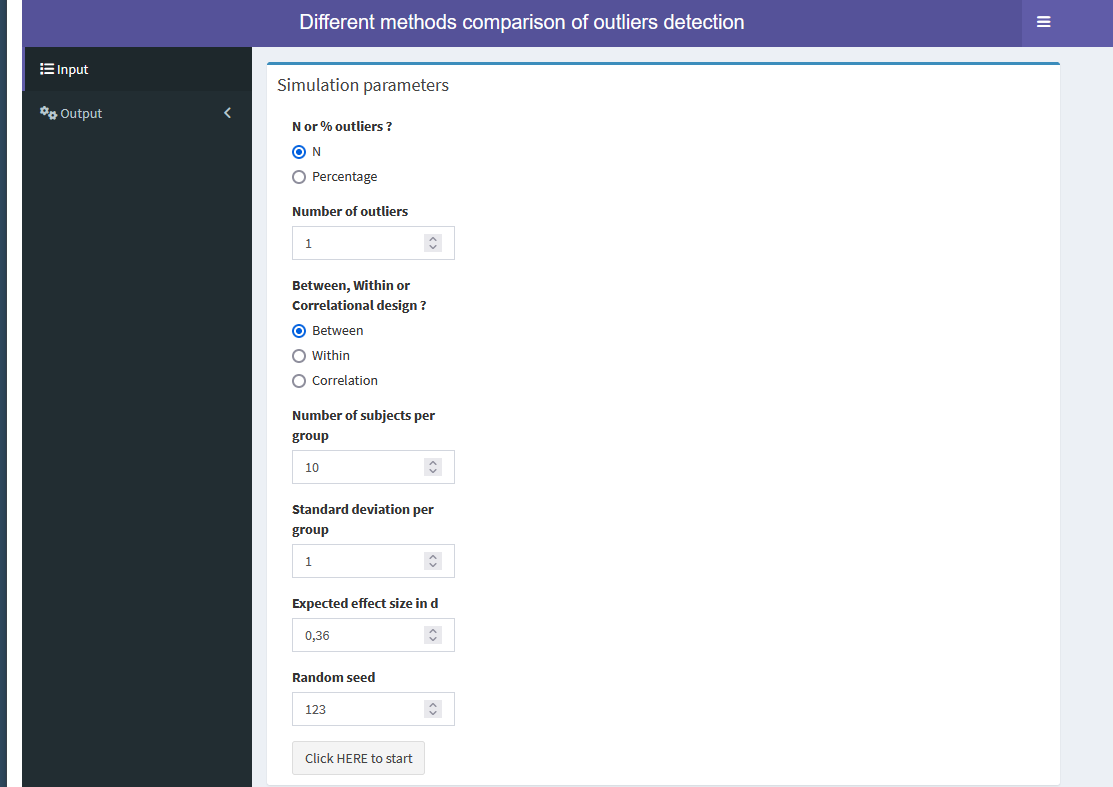
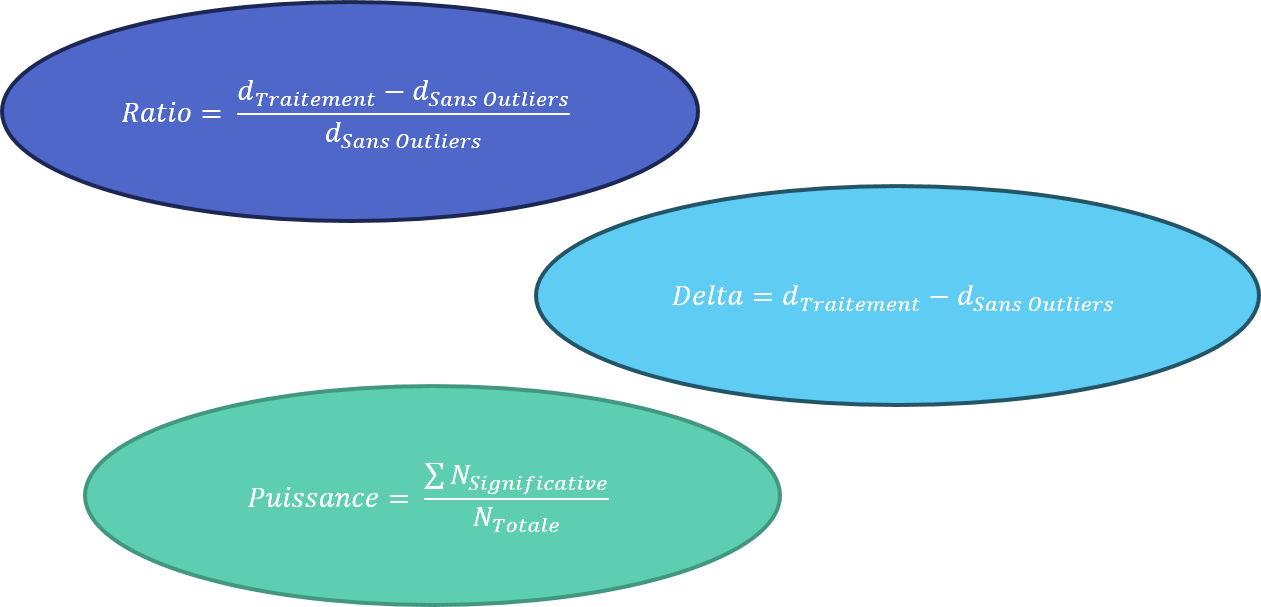
Première partie : Outliers dans le cas de designs simples

Résultats :

C’est mieux d’avoir un “grand” échantillon
Toutes les méthodes augmentent erreur Type I
Méthodes basées sur la médiane sont robustes (retrouvent les valeurs de départ)
Méthodes basées sur la moyenne sont biaisées (ne retrouvent pas les valeurs de départ)
Méthodes basées sur les RSS sont biaisées (ne retrouvent pas les valeurs de départ)

Deuxième partie : Outliers dans le cas de designs multivariés

La plupart des méthodes se basent sur les modèles (résidus)

\[y = \beta0 + \beta1x1 + \epsilon\]

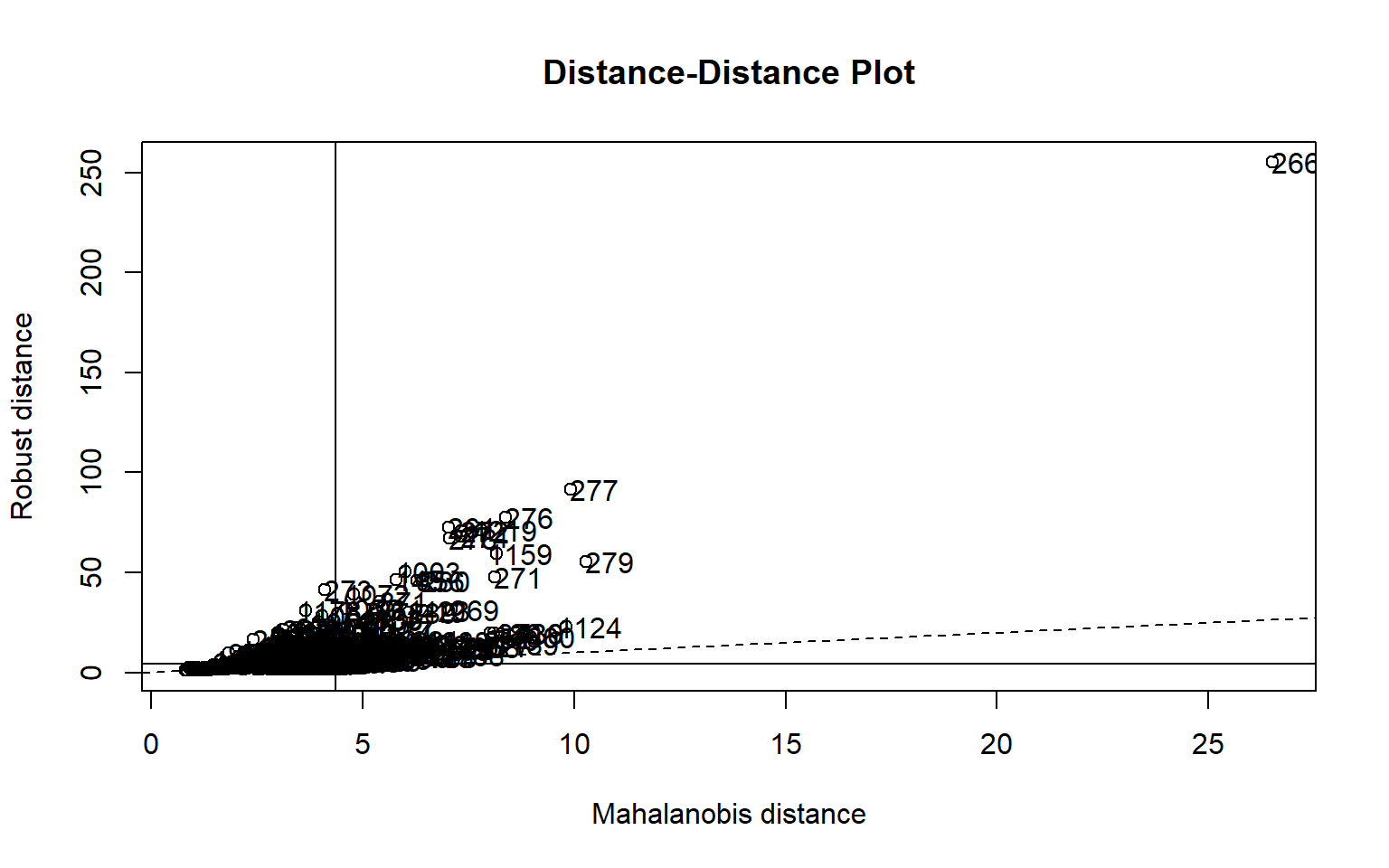
Deuxième partie : Outliers dans le cas de designs multivariés

Comment rendre compte des multioutliers en s’extrayant du modèle ?

Modéliser l’erreur autrement (Carroll et al., 2006) La solution n’est pas statistique mais méthodologique
Utilisation des modèles méchanistiques et non stochastiques (Lee et al., 2017)
Méthodes par bootstrap (mais il faut beaucoup de données)
Méthodes bayésiennes (mais il faut un prior)

En créant des modèles insensibles aux valeurs extrêmes

Deuxième partie : Outliers dans le cas de designs multivariés

Comment rendre compte des multioutliers en s’extrayant du modèle ?

En adaptant les données et non le modèle : Transformations (Tukey)

Troisième partie - méthodes de détection alternatives

Package performance (Lüdecke et al., 2021)

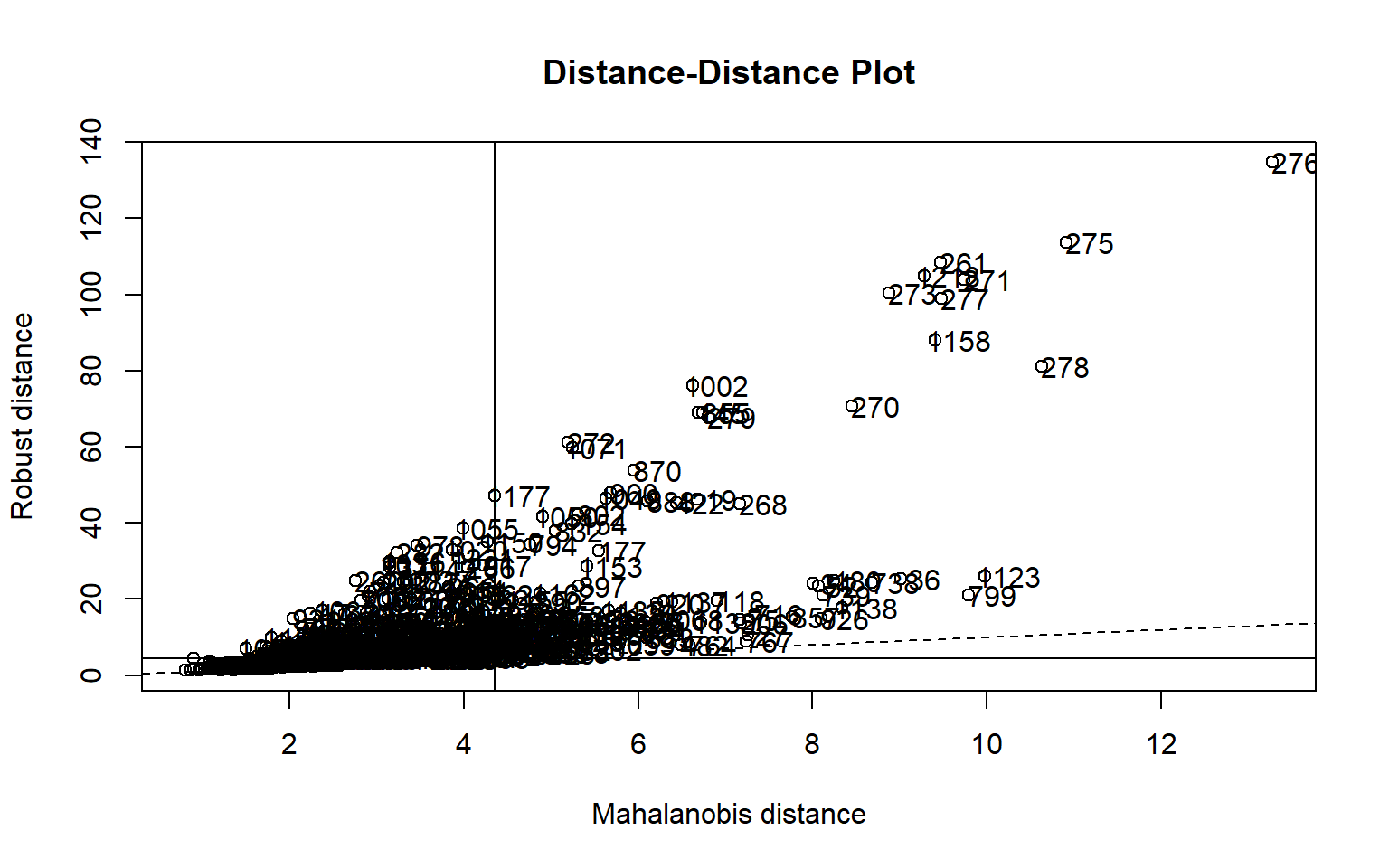
Mahalanobis & MCD :

Mahalanobis (Version historique)
Version robuste, c’est une correction
MCD (Leys et al 2018) ; Ajoute de l’info aux 2 précédentes en intégrant les covariances avec les autres résidus du modèle

Troisième partie - méthodes de détection alternatives

Package performance (Lüdecke et al., 2021)

Méthodes de réduction de dimension (clustering) :

Clustering (OPTICS ; DBSCAN)
Local outlier factor (basé sur k-means)
ICS (sorte d’acp)

Troisième partie - méthodes de détection alternatives

Package DHARMa : (Hartig, F., 2024)

Approche par simulation

Pour conclure

Plusieurs recommandations (Leys et al., 2019) :

Pré-enregistrement des analyses des outliers,
Report des analyses avec et sans
Améliorer la transparence :
- Sur les méthodes de détection des valeurs extrêmes
- Sur le traitement effectif des outliers (retrait ou non et pourquoi)

Merci de votre attention

Echanges et discussions

Références

Aguinis, H., Gottfredson, R. K., & Joo, H. (2013). Best-practice recommendations for defining, identifying, and handling outliers. Organizational Research Methods, 16(2), 270–301. https://doi.org/10.1177/1094428112470848
André, Q. (2022). Outlier exclusion procedures must be blind to the researcher’s hypothesis. Journal of Experimental Psychology: General, 151(1), 213–223. https://doi.org/10.1037/xge0001069
Carroll, R. J. et al.,(2006) Measurement error in nonlinear models, 2nd ed. London: Chapman & Hall.
Cowell, F. A., & Victoria-Feser, M.-P. (1996a). Robustness Properties of Inequality Measures. Econometrica, 64(1), 77–101. https://doi.org/10.2307/2171925
Cowell, F.A., & Victoria-Feser, M. (1996b). Poverty measurement with contaminated data : a robust approach. European Economic Review, 40, 1761-1771.https://doi.org/10.1016/0014-2921(95)00048-8
Grubbs, F. E. (1969). Procedures for Detecting Outlying Observations in Samples. Technometrics, 11(1), 1–21. https://doi.org/10.1080/00401706.1969.10490657
Hartig, F., (2024). DHARMa: Residual Diagnostics for Hierarchical (Multi-Level / Mixed) Regression Models. R package version 0.4.7, http://florianhartig.github.io/DHARMa/.
Hawkins, D. M. (1980). Identification of Outliers. Chapman and Hall.
Hlasny, V. and Verme, P., (2018) Top Incomes and Inequality Measurement: A Comparative Analysis of Correction Methods Using the EU SILC Data, Econometrics 6(2):30, June 2018., http://dx.doi.org/10.2139/ssrn.3162773
Karch J. D. (2023). Outliers may not be automatically removed. Journal of experimental psychology. General, 152(6), 1735–1753. https://doi.org/10.1037/xge0001357
Lee, Y., Nelder, J. A., & Pawitan, Y. (2017). Generalized linear models with random effects: Unified analysis via H-likelihood (2nd ed.). CRC Press
Leys, C., Klein, O., Dominicy, Y., & Ley, C. (2018). Detecting multivariate outliers: Use a robust variant of the Mahalanobis distance. Journal of Experimental Social Psychology, 74, 150–156. https://doi.org/10.1016/j.jesp.2017.09.011
Leys, C., Delacre, M., Mora, Y. L., Lakens, D., & Ley, C. (2019). How to classify, detect, and manage univariate and multivariate outliers, with emphasis on pre-registration. International review of social psychology, 32(1). https://doi.org/10.5334/irsp.289
Lüdecke et al., (2021). performance: An R Package for Assessment, Comparison and Testing of Statistical Models. Journal of Open Source Software, 6(60), 3139. https://doi.org/10.21105/joss.03139
Thériault, R., Ben-Shachar, M.S., Patil, I. et al. Check your outliers ! An introduction to identifying statistical outliers in R with easystats. Behav Res 56, 4162–4172 (2024). https://doi.org/10.3758/s13428-024-02356-w